数据结构——树状数组 Binary Indexed Tree

发表于 | 分类于

树状数组(binary indexed tree)能够高效地获取数组的子段和。 一般来说，树状数组可以用于解决数组子段和的动态查询或高效查询问题。

传统的数组单点修改的复杂度为\(~O(1)~\)，查询子段和的复杂度为\(~O(n)~\)。 而树状数组的修改和查询子段和复杂度均为\(~O(\log n)~\)。 所以在多组查询或动态查询时，用树状数组可以有效减小耗时，提高程序效率。

树状数组的操作

构建

从已知数组构建树状数组就是把线性的数组变成一棵树。那么，树状数组是如何把线性结构的数组变成一棵树的呢？以下以一个长度为8的数组为例：

原始数组：

1
A[1], A[2], A[3], A[4], A[5], A[6], A[7], A[8]

在修改和查询子段和时，很容易想到一种类似二分的想法来构建一棵树状的数组来保存原数组的所有信息。 用这种方法构造出的数组具有如下的结构：

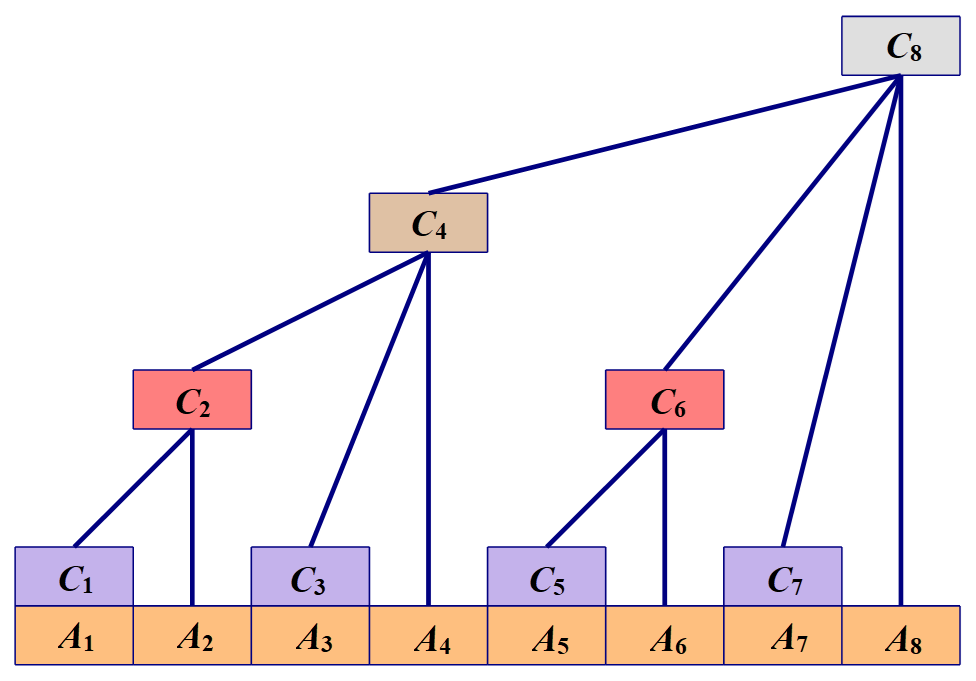
树状数组示意图

这样的一棵树满足如下的条件：

  • \(C_1=A_1\)
  • \(C_2=A_1+A_2\)
  • \(C_3=A_3\)
  • \(C_4=A_1+A_2+A_3+A_4\)
  • \(C_5=A_5\)
  • \(C_6=A_5+A_6\)
  • \(C_7=A_7\)
  • \(C_8=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8\)

从中可以发现，若结点的标号为\(~n~\)，则该结点的求和区域长度为\(~2^k~\)，此处的\(~k~\)为\(~n~\)的二进制表示的末尾\(~0~\)的个数。 由于\(~n~\)号结点求和区域的最末一位一定是\(~A_n~\)，于是有：

\[ C[n] = \sum_{i = n - 2^k + 1}^{n} A[i] = A[n-2^k+1]+A[n-2^k+1]+\cdots+A[n-1]+A[n] \]

于是构建树状数组的问题就变成了如何求\(~2^k~\)的问题。 利用位运算的性质，有一个非常漂亮的解答（\(\oplus\)表示异或）：

\[2^k=n\&(n\oplus (n-1))=n\&(-n)\]

这就是树状数组构建的核心：lowbit()函数，代码如下。

1
2
3
4
int lowbit(int x)   
{   
    return x & (-x);   
}

单点修改

树状数组的单点修改过程很简单：修改需要修改的点，然后沿着树上的路径把受到牵连的点一并修改。 由于树高为\(~O(\log n)~\)，故复杂度\(~O(\log n)~\)。 示例代码如下：

1
2
3
4
5
void add(int x, int y) // 在x位置上加上y
{
    for(int i = x; i <= n; i += lowbit(i)) // 找到与x相关的所有位置
        c[i] += y;
}

求前\(~n~\)项和

求前\(~n~\)项和时，由于在\(~C_n~\)记录了下标从\(~n-lowbit(n)+1~\)到\(~n~\)的子段和，故可以直接在结果中加上\(~C_n~\)，接下来只需要计算\(~C[n-lowbit(n)]~\)的值。一直循环下去即可。 由于树高为\(~O(\log n)~\)，故复杂度\(~O(\log n)~\)。

1
2
3
4
5
6
7
int sum(int x) // 前x项和
{
    int ret(0);
    for(int i = x; i >= 1; i -= lowbit(i))
        ret += c[i];
    return ret;
}

二维树状数组

其结构与普通的树状数组相同，只不过在求前\(~n~\)项和时是从\(~(1,1)~\)到\(~(x,y)~\)求和。 示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int lowbit(int x)
{
	return x & (-x);
}
void add(int x, int y, int val) // 将[x][y]的值增加val
{
	for(int i = x; i < N; i += lowbit(i))
		for(int j = y; j < N; j += lowbit(j))
			sum[i][j] += val;
}
int sum(int x, int y) // 求以[1][1]为左上角端点,[x][y]为右下角端点的矩阵和
{
	int ret(0);
	for(int i = x; i > 0; i -= lowbit(i))
		for(int j = y; j > 0; j -= lowbit(j))
			ret += sum[i][j];
	return ret;
}

树状数组的应用

  • 动态查询子段和——HDU 1166 敌兵布阵；
  • 求逆序数——HDU 1349 Minimum Inversion Number；

练习题目

  • POJ 1195 Mobile phones
  • POJ 2481 Cows
  • POJ 2155 Matrix
  • POJ 3321 Apple Tree
  • HDU 1556 color the ball
  • POJ 2299 Ultra-QuickSort